Seasonal Uncertainty

Update, Thursday, December 3, After the Bell

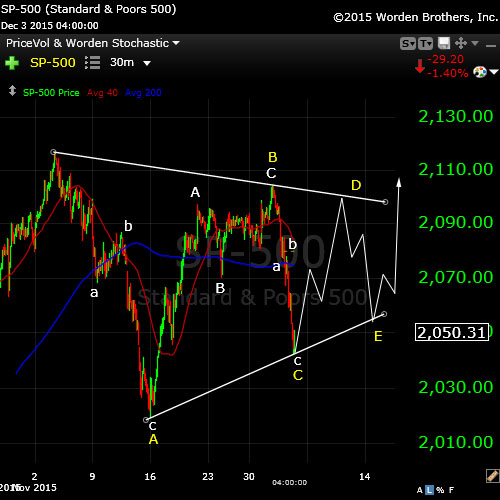
Here’s a quick look at the SP500 (30 minute chart). You can see it’s tracing out a large fourth wave triangle. All the waves so far are in 3 and the remaining waves should be also. The final wave up may either go to the previous high or may go up much further. I will do some measurements to try to find a range.

This puts well into next week to finish up the pattern. This fourth wave triangle signals that there is one more wave only after the triangle to finish up this larger C wave.

___________________

Update Thursday, December 3, Before the Bell

With Draghi’s announcement of more easing, the currencies seem to have changed direction. The eur.usd should now come down 62% to complete a second wave and then head back up again.

Meanwhile, futures have dropped without technical damage. They’re moving together with currencies inversely (as they have for a few months) so my guess is that during this second wave action in currencies, we may see futures and cash complete a double top.

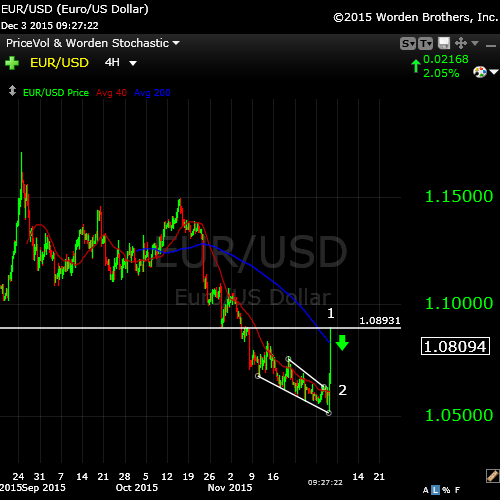
Above, a 4 hour chart of the eurodollar. You can see the ending diagonal complete this morning and the first wave up complete. It should back off 62% in a second wave before taking off again.

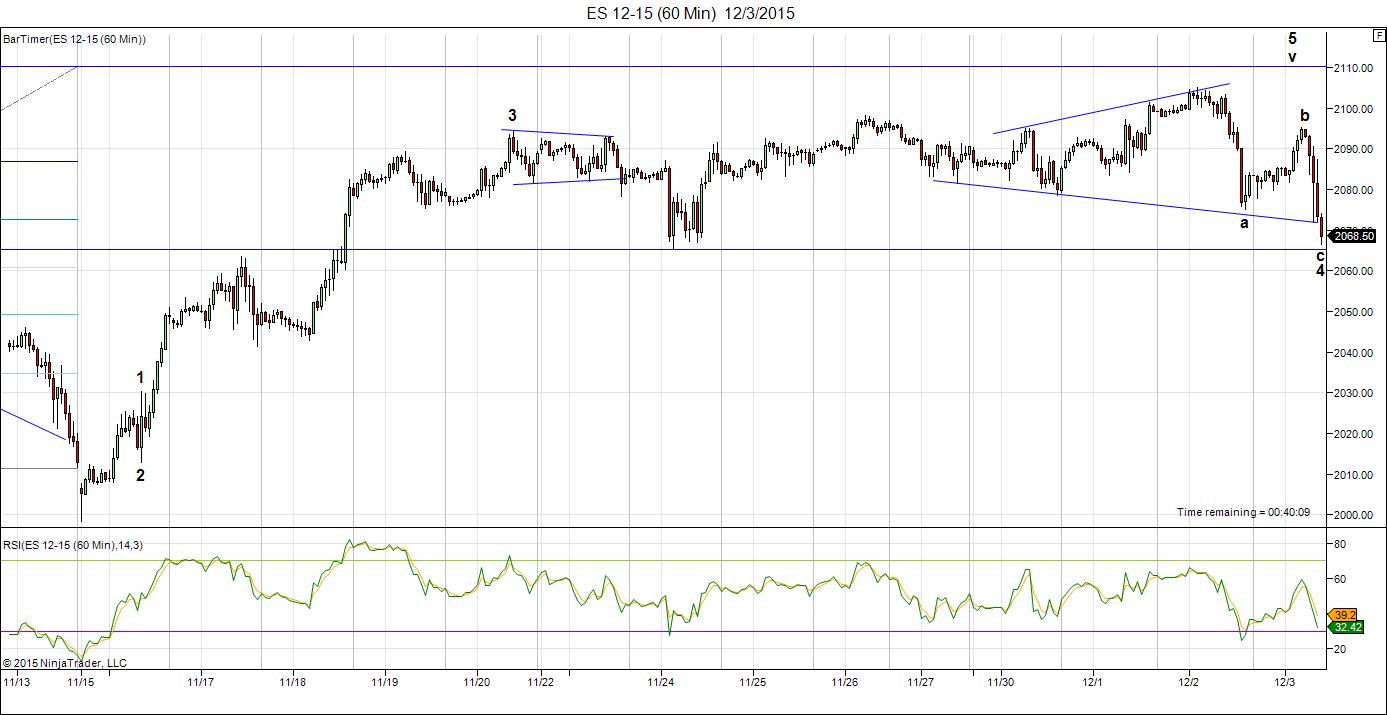
Above is the count on ES (60 minute chart) as of this morning. We have a second leg of a fourth wave forming, by the looks of it. This sets us up for the fifth wave up and the triangle disappears.

No more trying to update charts intraday. The problem is trying to label charts in transition—they’re still defining the pattern.

NQ appears in a channel and may have completed 5 waves up. They have all come down in 3 waves so far, so the target is still up.

Let’s see what happens.

_____________________________

Update Tuesday, Dec. 1 After the Bell

Tonight, I’ve updated the top two charts (SP500 and ES). There isn’t much point creating a new blog as very little is changing day to day. Currencies continue to work towards a bottom and the equities slowly trace out the final wave up.

Possible triggers this week:

• Yellen Speech: Janet Yellen, 12:25 EST, Wednesday, Dec.2
• Yellen Testimony Congress: Thursday, Dec 3, 11am EST
• ECB Press Conference: 14:30 CET (8:30am EST), Thursday, Dec 3
• Latest US Labor Report: 6:30am EST, Friday, Dec. 4
• Fed Meeting: December 15-16

The latest count for ES and SP500:

ES on the 60 minute chart (SPX futures) has traced out a 4th wave and we’re now working on the final 5th wave. I tossed out the triangle, as the final leg down ended up short. This pattern should result in an eventual test of the previous high at 2110. We’ve completed a small second wave within this last wave up and appear to be working away at the third wave.

It’s a similar count to the cash index of the SP500.

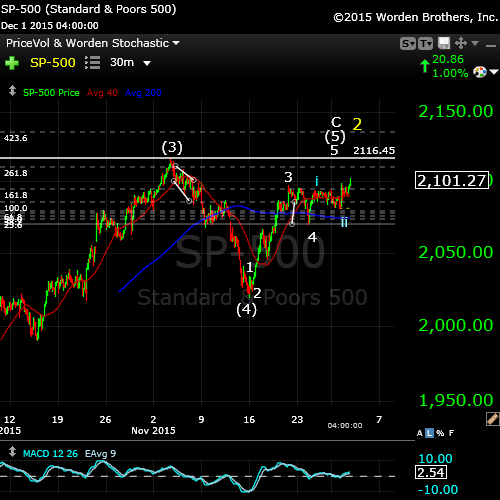
Here’s the 30 minute chart for the SP500. The final wave up continues to unfold … slowly. The SPX is in the same position as ES at the end of the day (Tuesday). We’re in a third wave of the 5th of the 5th.  That would leave a tiny 4 and 5 after that up to the previous high at 2116.48.

Friday (Nov 27) was 97 days from the low of Aug, 24, which is 97 days from the all time market high of May 20, 2015.

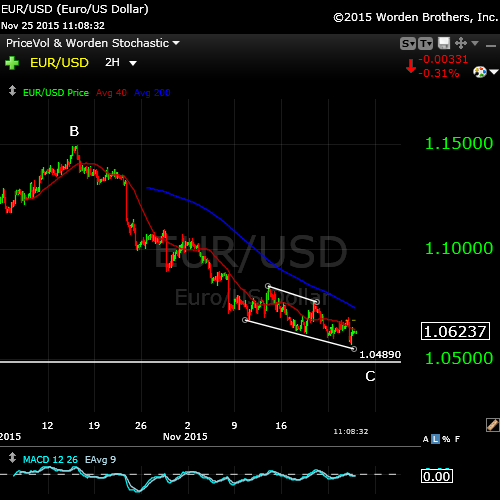
Above is the Euro/dollar currency pair. You can see the final patter playing out: an ending diagonal. The US dollar chart shows the same pattern. All the US dollar currency pairs are about the reverse at the same time the equities market tops.

An  ending diagonal is a terminal pattern that ends a motive set of waves or a corrective C wave. It’s the “end-of-the-line” and results in a dramatic reversal.

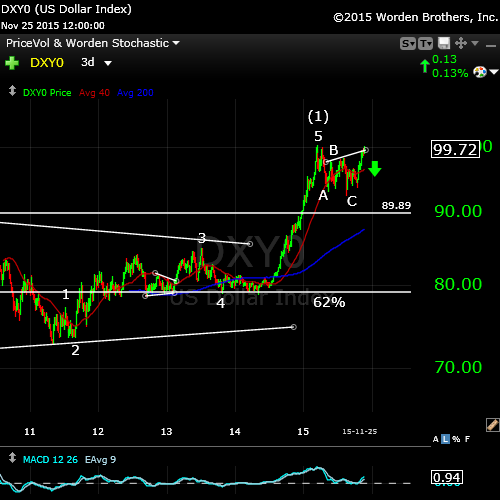
Here’s the dollar:

And finally, here’s a really super set-up, the pound/dollar.

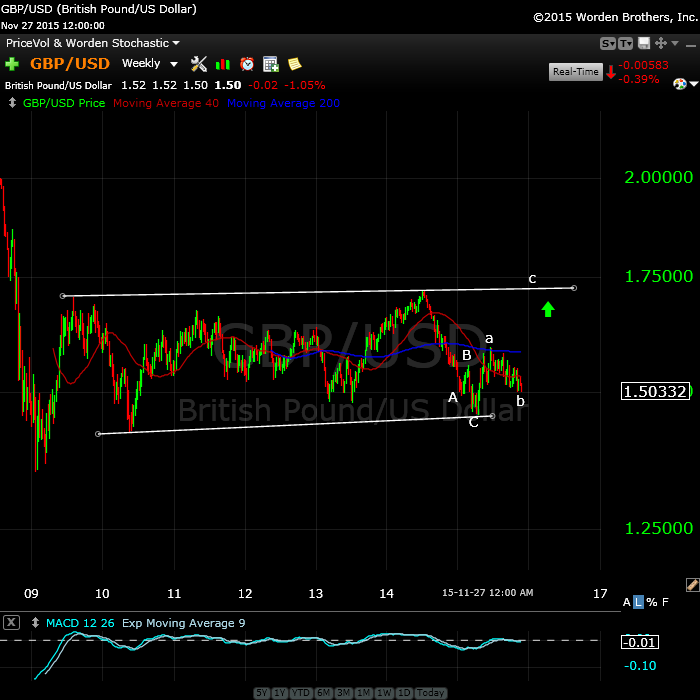
If you like trading currencies, here’s a no brainer. The GBP/USD weekly chart shows a large 4th wave triangle. We have a C wave left to go on the last leg of the triangle (the e leg) and then we should turn down into a fifth wave. I’ve been watching this one off and on for quite a while.

____________________________

Original Post:  The Question of Seasonal Bias

I want to address a couple of issues here right off the bat.

The Decennial Cycle (chart below) that’s thrown around without a lot of thought is not a “cycle” in the true sense of the word. It a short-term phenomenon, or pattern, perhaps. It’s interesting that most charts only go back a few decades to make the case for a continuing pattern.

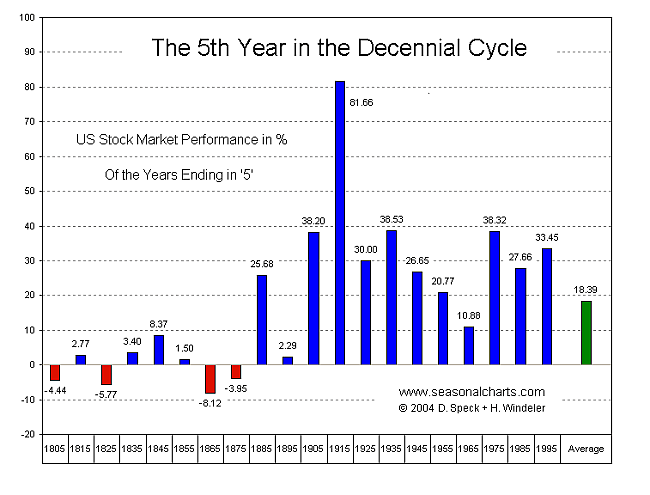
The chart above goes right back to 1805 so you can see the issue I have with this phenomenon being anything other than a short-term pattern. 2005, in fact was ‘flat’ or negative, depending on who you listen to. So far this year, the NYSE is down one percent. I find the reference to the “decennial cycle” lacking in any kind of credibility.

You’ll find the article to this chart here.

In terms of seasonal bias, Santa Claus and end of year seasonal rallies show even a spottier performance. On the other hand, as a contrarian, I would much rather see rabid optimism in the market, as we have now. In my way of thinking, it sets up the perfect scenario.

A Wave-Following Fool!

That’s what I basically am. I haven’t found a time when Elliott Waves have lied to me. It always ends up being a weakness on my part if I get a count wrong. The waves always do the predictable thing, very often in an unpredictable manner.

Cycles are important for identifying turn dates. It could be argued that they haven’t been very predictable lately. There’s some truth to this, but keep in mind that we’re dealing with an unnatural market (influenced by central banks around the world). Cycles are natural phenomena. You can fight them only for so long. Eventually they’ll take control again.

We’re looking at November 23rd to 25th (full moon) as possible turnover days. The wave structure forecasts a turn. Converging cycles (I cover this below) are also pointing to the very near future for a trend change.

It’s interesting to note that the period between the May 20, 2015 market high and the low on Aug. 24 is 97 days. Taking that same timeframe from Aug 24 (97 days) takes us to Nov. 27 (this coming Friday).

Bottom Line: We’re in the final fifth wave up looking for a double top, turning over into wave three down.

Here’s 15 minute chart of the SP500 from the market close on Friday. There are a couple of ways of counting this wave up, but nonetheless, I put us in the final 5th subwave heading for the previous high of 2116.48. We may either be tracing out a traditional motive 5th wave or heading into an ending diagonal. There are signs in the futures that we’re in the midst of the latter, but the end result will be the same.

Backing out the chart of the SP500 (1 hour bars), we can see the larger pattern playing out. This is an expanded flat scenario, which is a set of corrective waves in an ABC (3-3-5) configuration. You can see we’re in the final stage of the C wave.

What’s particularly interesting about the ending of this wave is that the fourth wave dropped to exactly 1.618 times the length of the first wave, which is the usual length for a 5th wave. It also dropped to the previous 4th wave. It always amazes me as to how organized the market is.

This forecasts the probability that the fifth wave will stop at the previous high (2116.48) and turn down.

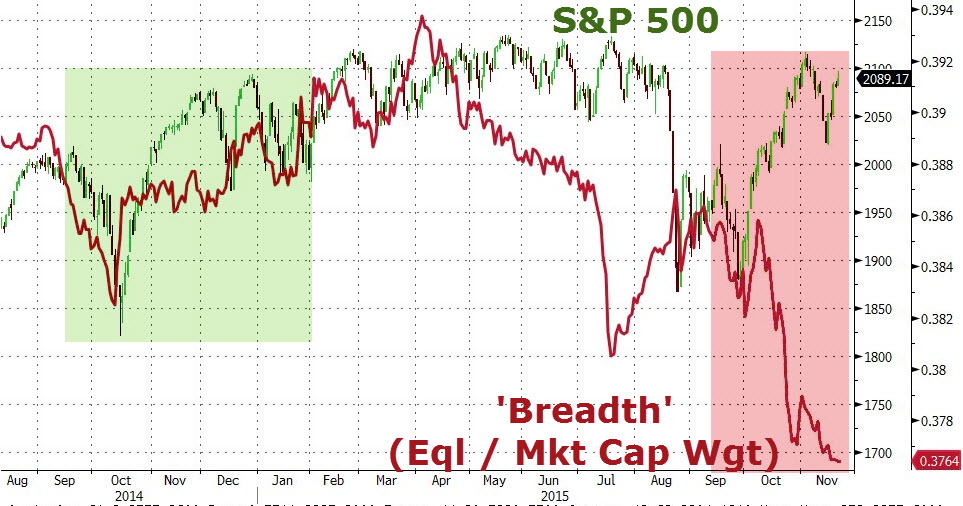
Above you’ll find a snapshot of market breadth, which continues to implode. This is from today’s zerohedge blog post.

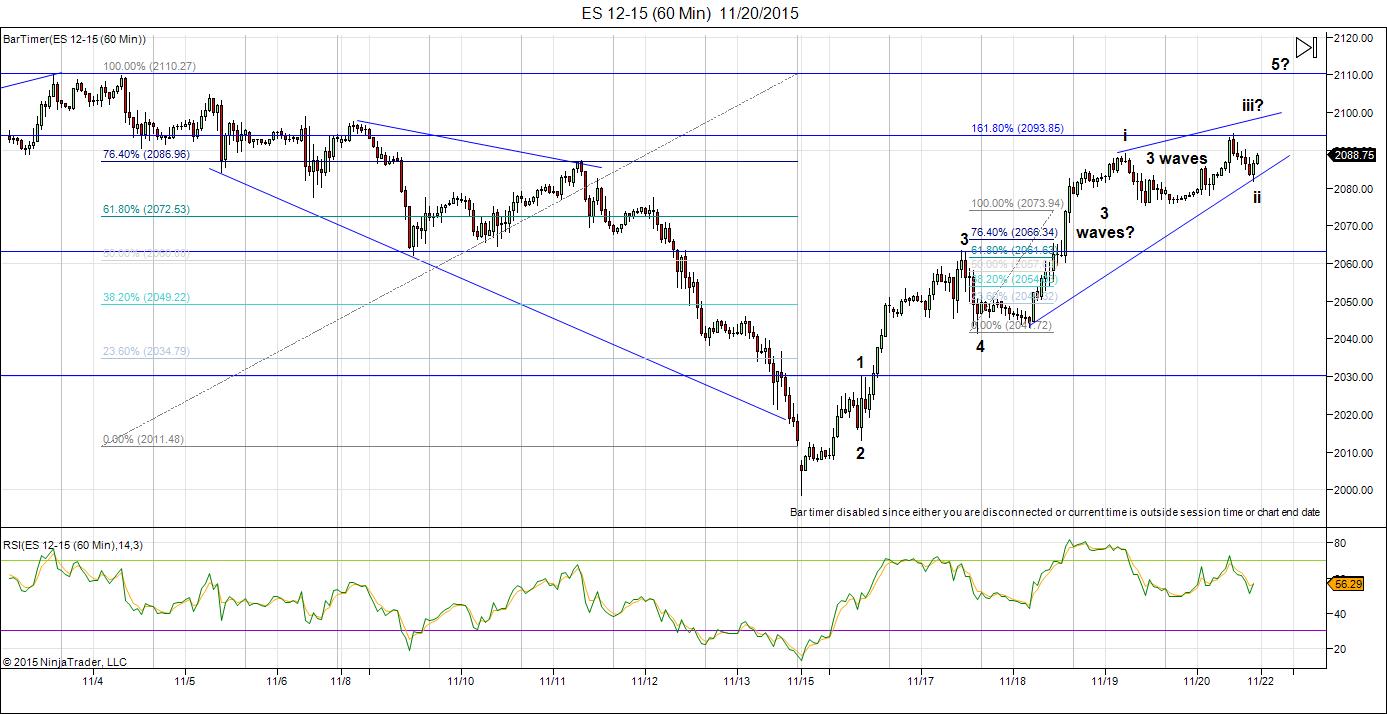
This is the one hour chart of the ES (SP500 futures). I’ve labelled the waves, which are much easier to decipher here than in the cash indices. Look at the final waves. The segment after my i label is definitely in 3 waves and the wave up before it also looks like 3 waves, but I can’t be as certain about that. This would suggest an ending diagonal, a wave in 5 subwaves, each wave of which is 3 waves (3-3-3-3-3). This is an ending wave and if this is what continues to trace out, it should give early warning of a top.

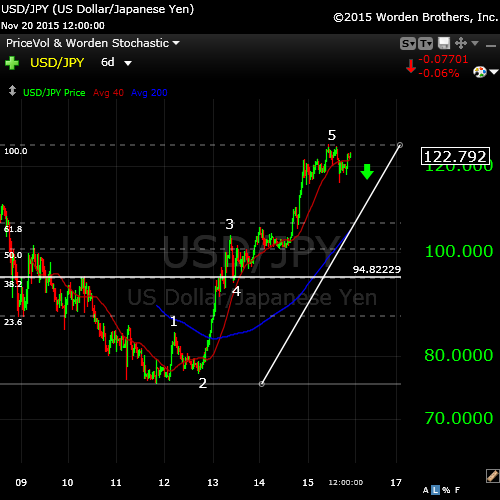
Currencies have turned, or are in the midst of turning. This is the 6 day chart of USD/JPY. It shows the first motive wave up from 2012. You can see that it’s complete five waves up. It needs to retrace in a second wave down and, in fact, has already turned. It appears to have completed one wave down, one up, and is set to start the C wave down. I would expect this wave to retrace 62% (the horizontal line).

This reinforces the “All the Same Market” idea that I’ve shown in previous posts. In fact, all the US currency pairs have either turned up or will do so in a matter of hours or days. There are some very good opportunities setting up here.

Now on to cycles:

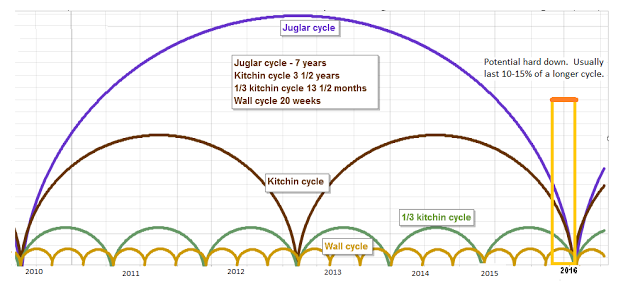
Here’s a chart of the Juglar, Kitchin, and Wall cycles which are harmonic. They’re forecasting a turn near the end of 2015 or very early 2016. More specifically, they point to the January/February time period as a bottom.

You can find this chart and a full explanation at http://swingcycles.blogspot.ca.

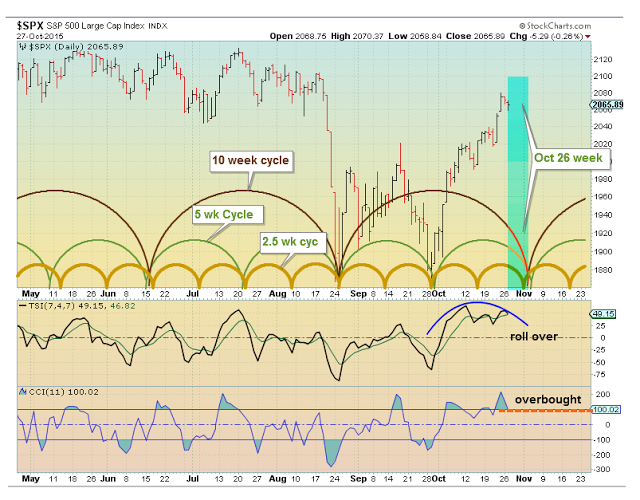
This is a similar chart of the recent past. You’ll see the end October/beginning of November forecasting a major top. In fact, we topped in wave 3 of C on November 4—a direct hit.

Andy Pancholi’s “Market Timing Report” forecasts November 23 as the major turn point for the month. I highly recommend it for its accuracy. You can find it here.

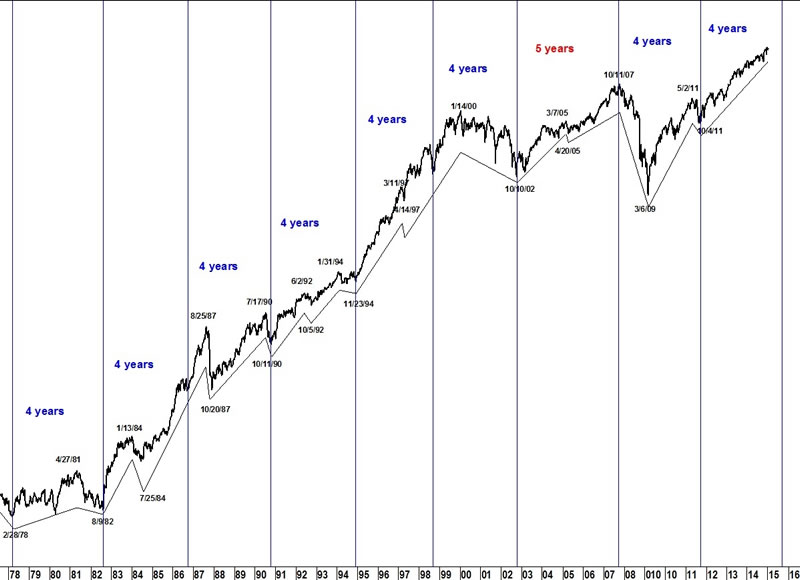
On a longer-term basis, here’s a look (above) at the 4 year cycle on the DOW. This cycles forecast looks to the end of 2015 for the turn. You can see how long-term and persistent this cycle is.

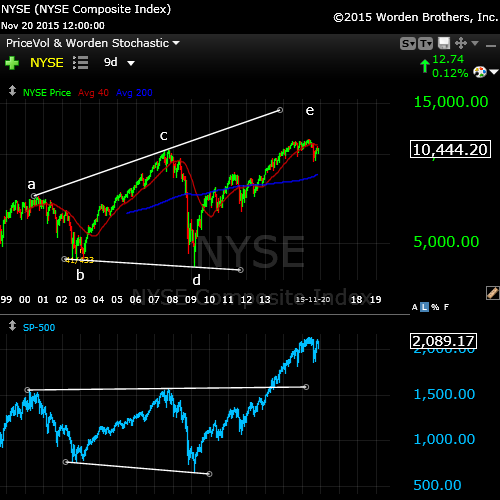
I was asked this week about the broadening market topping pattern (well-known market topping pattern—not Elliott Wave related), so decided to include it here.

Above is the larger broadening top of the NYSE in a 9 day chart going back to 1999. This would be called an “ending expanding diagonal” in EW terms. It’s an extremely bearish pattern and seem to be failing in the final stages.

It’s interesting to me to note the difference in the NYSE as opposed to the SPX (lower blue chart). It speaks to the breadth of the market. It tells me the buying is concentrated in the big cap stocks.

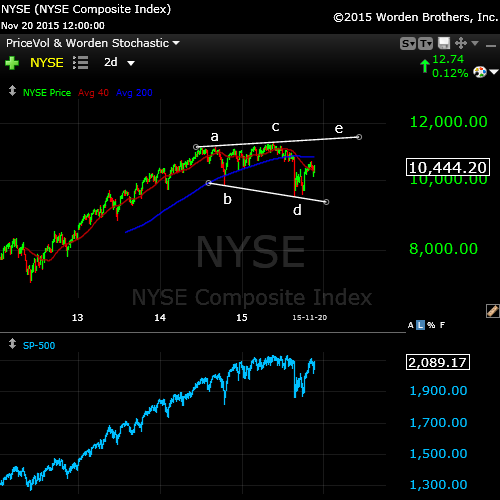
Above, we can see this same pattern on a short term scale in the final wave of the larger topping pattern. We have what appears to be a failing e wave in the NYSE 2 day chart.  

There’s also a non-confirmation here, as well. with the SPX chart. This suggests the rally is narrow on even a short term-basis, with most of the buying in the big cap stocks.

DOW Theory (Transports and Industrials Non-Confirmation)

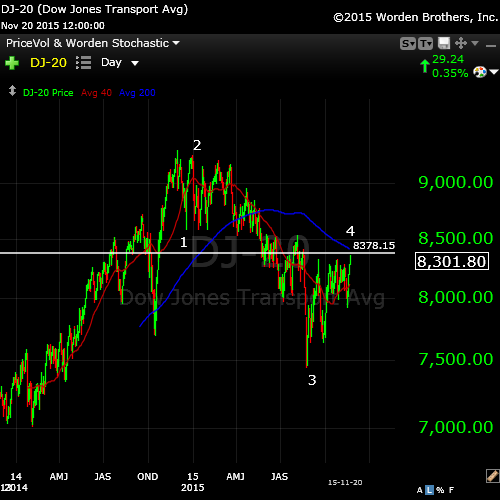
I haven’t brought up the Dow Transports non- confirmation for a while, but it’s been busy at work setting up for the next drop. The Transports Index (DJ-20) is tracing out a typical fourth wave (above), with the Industrial Index finishing off the 2nd wave (below). Both are setting up for a turn down in tandem. You can find background on the DOW Theory here.

For more confirmation, you can visit this article on the Baltic Dry Freight Index. Scary stuff!

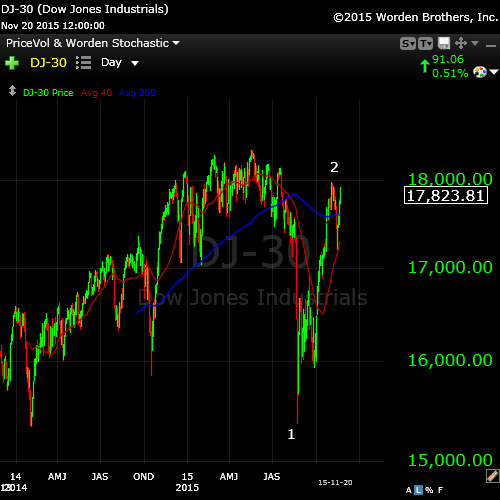
Above is the daily chart of the DOW, showing us at the top of wave 2.

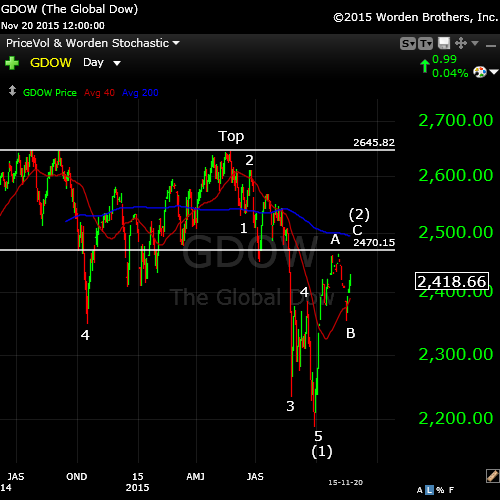
Next to last, here’s a daily chart of the Global DOW. Not much has changed here lately.

The Global DOW is like the elephant in the room, letting you know what’s happening on an internationalk basis. We’ve completed one set of motive waves down from mid 2014 and have retraced exactly 62% in a second wave, where we sit now. Actually, we’re completing a fifth wave up in this second wave rally, which should top at the same time as the US equities roll over. The writing is on the wall!

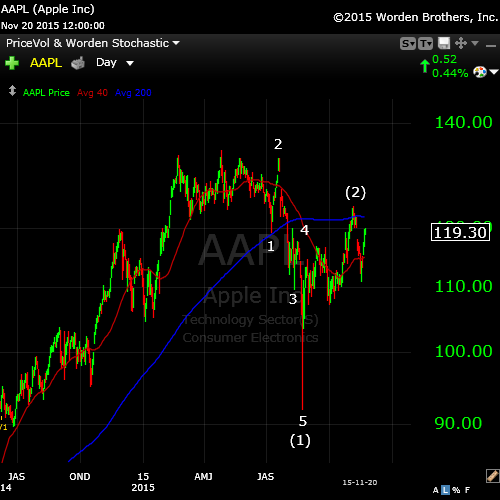
Finally, a daily chart of Apple Computer. Here’s a textbook Elliott Wave set-up, with absolutely perfect fibonacci measurements. We completed one wave down of 5 motive waves and retraced more than 62% bin an ABC second wave. The third wave down is 1.618 X the length of the first wave, which the fifth wave is a similar length. Nothing like hitting me over the head with an Apple bat!

The final small wave up will either turn over now or head up to test the top at (2) before rolling over into a third wave down.

There are a lot of stocks setting up in similar manner out there …

It should be an interesting week coming up, both with equities and currencies. Stay safe and profitable.